8 concepts de base pour quantifier l’expérience utilisateur

Vous n'avez pas besoin d'être un mathématicien pour quantifier les problèmes et les améliorations que vous pouvez réaliser sur une interface destinées aux utilisateurs.

La plupart du temps, les mesures les plus convaincantes peuvent être réalisées très simplement : vous n’avez besoin que de connaître l'arithmétique et l'algèbre de base.

La majorité d'entre nous a étudié ces concepts pendant vos années de 4ème et de 3ème. Mais on les oublie facilement et on peut difficilement les appliquer, surtout lorsqu’ils ne sont pas situés dans le contexte dans lequel nous les avons appris.

Voici huit concepts fondamentaux qui vous aideront à quantifier l'expérience utilisateur.

Convertir les pourcentages et les proportions

Une « proportion » est ce qui cela semble être : la partie d’un total. Si 8 utilisateurs sur 10 peuvent localiser un objet dans votre navigation, alors la proportion est de 8/10 = 0,8. Elle est généralement exprimée en pourcentage. Pour l’obtenir, il faut bouger la décimale à droit de de crans (multipliant ainsi la proportion par 100). De ce fait, 0,8 devient 80% : le taux de réussite est donc de 80%. Vous pouvez également soustraire 1 à votre proportion : 1-0,8 = 0,2. Convertissez-le en pourcentage et vous obtiendrez votre taux d’échec, qui est de 20%.

Les pourcentages peuvent être utilisés sur n'importe quelle taille de l'échantillon

« Pourcentage » signifie littéralement « pour 100 ». On considère généralement qu’il faut avoir un grand échantillon (plus de 30 ou de 100) pour utiliser les pourcentages. Mais vous pouvez utiliser les proportions et les pourcentages pour n’importe quelle taille de l’échantillon. Si cette dernière est trop petite, elle risque cependant de ne pas correspondre à la réalité. Les intervalles de confiance peuvent être utilisés pour n’importe quel pourcentage : ils permettent de fournir le taux le plus plausible de la proportion de la population inconnue.

Pour exprimer une augmentation ou une diminution d’une valeur, utilisez la technique ci-dessous

Commencez par soustraire la nouvelle somme à l’ancienne somme. Divisez le résultat par l’ancienne somme. Par exemple, si le temps moyen que les utilisateurs prennent pour s’inscrire à un site Internet passe de 100 secondes (ancienne somme) à 70 secondes (nouvelle somme) avec le nouveau design, le temps nécessaire pour s’inscrire a été réduit de 30%.

(Ancienne somme – Nouvelle somme)/ Ancienne somme

( 100 – 70 ) / 100 = 0,3 ou 30%, exprimé en pourcentage.

Vous pouvez également calculer à quel point l’ancien temps nécessaire pour s’inscrire était plus long que le nouveau. On prend les mêmes valeurs, mais on les inverse.

( 70 – 100 ) / 70 = -,429 ou -43%.

Les pourcentages négatifs sont assez difficiles à interpréter. Je prends donc le chiffre de « -43% » et je dis que les utilisateurs prenaient 43% de temps en plus pour s’inscrire avec l’ancien design du site Internet. Ce sont deux façons différentes d’exprimer la même chose, mais le premier calcul est le plus commun.

Les pourcentages d’augmentation sont différents des points de pourcentage d’augmentation

En passant de 30% à 33%, vous augmentez de 10%, mais de seulement 3 points de pourcentage. Le taux d’augmentation que vous choisissez dépend de votre motivation et de celle de votre auditoire. La plupart des gens confondent une hausse de 3 points avec une hausse de 3%. Une augmentation de 3 points ne semble pas aussi impressionnante qu’une augmentation de 10%. Sauf en ce qui concerne les taux d'achèvement et les taux de conversion, vous utilisez probablement l'augmentation de 10%. Si vous augmentez vos taxes, vous utiliserez l’augmentation de 3 points.

Ordre des opérations

L’équation la plus célèbre dans le domaine de l’utilisabilité est : 1 –(1-p) n. Il vous indique le pourcentage de problèmes avec une probabilité d'occurrence (p) que vous verrez quand vous aurez testé un certain nombre d'utilisateurs (n). Elle est basée sur la formule de probabilité binomiale et est au cœur d’un chiffre magique dans la planification de la taille de l'échantillon : le chiffre 5. Le p (parfois lambda) indique à quel point un problème d’utilisabilité est commun (exprimé en proportion). Par exemple, si un problème touche 1 utilisateur sur 3, p est de 0,333. La valeur « n » correspond à la taille de l’échantillon. Pour résoudre l’équation, partez de la parenthèse, faites une exponentiation et une soustraction.

Par exemple, si vous testez 5 utilisateurs, quelle chance avez-vous de détecter un problème qui affecte 31% des utilisateurs ?

1 –(1-,.31) 5

1 –(0,69) 5

1 – 0,1564

0,843597

Exprimez-le en pourcentage. Vous avez donc 84,4% de chance de détecter le problème en testant 5 utilisateurs. Si le problème n’affecte qu’un utilisateur sur 10, vous aurez 41% de chance de le détecter après avoir testé 5 utilisateurs.

Il y a beaucoup de « moyennes »

La moyenne arithmétique est la mesure la plus courante pour calculer une moyenne, mais la médiane et le mode sont d'autres mesures célèbres qui ont une « tendance centrale ». Les moyennes géométriques et harmoniques sont aussi fréquemment utilisées dans l’univers des sciences du comportement, mais sont moins connues du grand public.

La médiane peut être utilisée pour déterminer la donnée centrale d'un ensemble de données, quand il n’y a que peu de valeurs extrêmes, comme le prix des maisons dans une ville ou les salaires des employés d’une entreprise. La moyenne est extrêmement influencée par une seule grande valeur, alors que la médiane est beaucoup moins influencée par les extrêmes. Le graphique ci-dessous montre le temps dont 50 utilisateurs ont eu besoin pour localiser le magasin de location de voitures Budget le plus proche. La moyenne arithmétique est de 133 secondes et le temps médian est de 120 secondes. Si la moyenne est aussi élevée, c’est parce qu’elle est extrêmement influencée par les deux extrêmes de 350 secondes.

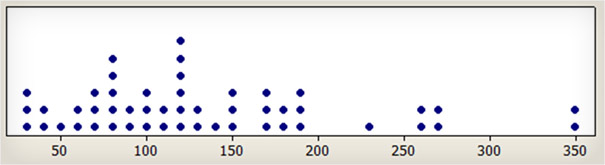
Image 1 : temps (en secondes) dont 50 utilisateurs ont eu besoin pour localiser le magasin de location de voitures Budget le plus proche . Le temps médian est de 120 secondes : il n’a pas été aussi influencé que la moyenne (de 133 secondes) par les deux utilisateurs qui ont pris beaucoup de temps.

Logarithme

C’est juste un exposant renversé. On l’utilise pour minimiser l'effet des valeurs extrêmes dans des données comme les salaires, les prix des maisons et le temps nécessaire pour réaliser une tâche. Il arrive très souvent que les utilisateurs les plus lents prennent 5 à 10 fois plus de temps pour réaliser une tâche que les plus rapides (comme dans l’exemple ci-dessus). Ces utilisateurs très lents tirent la moyenne arithmétique bien au-dessus du point central.

Les logarithmes sont effrayants, mais nous les utilisez plus ou moins naturellement. L’un des problèmes de ce mot est qu’il n’a plus vraiment de signification aujourd’hui. Qu’est-ce que le « log » et où est le « rythme » ? Utiliser le mot « ampleur » à la place du mot « logarithme » semble être pertinent. Mais la fameuse échelle de Richter, qui mesure la magnitude des tremblements de terre, est un logarithme.

Nous avons constaté que la moyenne géométrique est une meilleure façon de mesure une moyenne que la médiane, lorsque les échantillons sont inférieurs à environ 25. La moyenne géométrique peut être trouvée en prenant la moyenne des logarithmes, puis en les transformant.

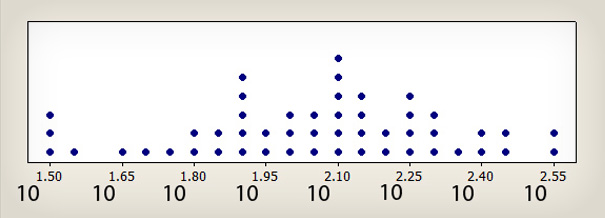
Image 2 : transformation logarithmique de l’image 1. La transformation logarithmique donne plus d’importance aux taux les plus élevés et permet de mieux déterminer le centre. Un temps de 350 secondes devient 2,54, qui est représenté par le chiffre 10 sous 2,54.

La majorité d’entre nous maîtrise les exposants

102 est 100 et 103 est 1 000. Un logarithme est l’inverse d’un exposant. Avec lequel des 10 premiers chiffres obtiendrez-vous 1 000 ? La réponse est : le chiffre 3. C’est vrai, le logarithme de 1 000 est 3. Si vous ne comprenez pas pourquoi, demandez-vous quelle ampleur vous obtiendrez 1 000. Rappelez-vous : c’est 10 puissance 3. La majorité des calculatrices possède un bouton pour calculer le logarithme. Sur Excel, vous pouvez utiliser la formule =LOG10().

L'écart-type et la variance sont interchangeables, mais sont légèrement différents

L'écart-type est très souvent utilisé pour calculer la variabilité. On peut le considérer comme le chiffre moyen qui sépare les différentes données de la moyenne. En mesurant la moyenne et la variabilité, vous pourrez décrire presque tous les ensembles de données. La variance est l'écart-type au carré.

De même que pour le pourcentage et la proportion, vous pouvez obtenir l’autre donnée en en possédant une. Alors que nous exprimons souvent la variabilité en utilisant l’écart-type standard, la variabilité est utilisée dans les formules elles-mêmes. Vous savez que vous ne pouvez pas y ajouter ou y soustraire des racines carrées… sauf si vous ne vous souvenez pas de votre cours d’algèbre de 3ème !

Librement inspiré de cet article.