Comment s’assurer une bonne confiance envers ses résultats ou “Pourquoi faire des tests quantitatifs avec un minimum de 100 personnes ?”

“Quelle valeur peut-on donner aux résultats obtenus ?”

Cette question revient souvent chez nos clients. Lors de la réalisation d’un test quantitatif (typiquement un sondage), les questions de fiabilité, de représentativité et de confiance envers les résultats observés sont, de manière légitime, régulièrement soulevées.

Voici quelques éléments de réponse, de quoi vous rassurer et/ou vous guider dans la réalisation de vos tests.

Commençons par quelques définitions, afin de clarifier ce dont nous parlons.

Fiabilité, représentativité et confiance

La fiabilité statistique correspond au degré de cohérence des résultats lorsque la mesure est répétée (sur plusieurs échantillons par exemple). Ce facteur est intrinsèquement lié au test en lui-même (formulation des consignes, types de mesures utilisées, sensibilité des échelles). Une manière de renforcer la fiabilité est d’utiliser des tests dits “standardisés” (par exemple l’AttrakDiff) et de faire appel à des experts du domaine pour construire votre test.

La représentativité dépend de l’échantillon, de sa constitution et de la sélection des participants. C’est en réalité l’échantillon qui est représentatif et non les résultats obtenus. On dit que l’échantillon est représentatif de la population parente de laquelle il est issu.

De cette représentativité va dépendre l’étendue des conclusions que vous allez tirer du test. Par exemple, si vous réalisez un test sur un échantillon de parisiens âgés de 25 à 40 ans, vous ne pourrez logiquement pas étendre vos conclusions à une population provinciale âgée de 20 à 60 ans ou à l’ensemble de la population française.

Le meilleur moyen de s’assurer une bonne représentativité de l’échantillon est de bien définir sa cible en amont du test et de sélectionner de manière aléatoire des répondants correspondants à cette cible.

Chez Testapic, nous nous assurons d’une bonne connaissance du profil de notre communauté afin de cibler au plus juste les répondants aux tests et d’obtenir des échantillons représentatifs des cibles souhaitées par nos clients. En revanche, personne d’autre que vous ne saurait déterminer la cible visée par vos tests (vos clients, vos prospects, vos utilisateurs…) !

La confiance envers les résultats obtenus se réfère directement à la valeur obtenue sur les mesures du test. La question sous-jacente pourrait être “les résultats obtenus à mon test sont-ils identiques à ceux qu’on aurait obtenus en interrogeant l’ensemble de la population parente ?”

Intervalle de confiance et marge d’erreur

L’intervalle de confiance se calcule en fonction du niveau de confiance (ou coefficient alpha “⍺”) que l’on souhaite avoir. Ce niveau de confiance n’est pas calculé mais est choisi a priori par l’analyste. Il représente le pourcentage de chance que l’intervalle recouvre la valeur réelle de la population parente si la mesure était répétée sur plusieurs échantillons. Ce niveau de confiance représente en d’autres termes “le risque de se tromper”.

Généralement on utilise un intervalle de confiance de 95%, IC(.95), soit : 95 chances sur 100 que la valeur “réelle” (de la population parente) se situe dans l’intervalle calculé.

Les bornes minimale (IC-) et maximale (IC+) de l’intervalle de confiance, autour de la valeur observée (une moyenne ou un pourcentage), sont déterminées par la marge d’erreur. De la marge d’erreur dépend ainsi la précision de la valeur estimée par l’intervalle de confiance.

Plusieurs facteurs influent sur la marge d’erreur et donc sur la précision de l’estimation ; nous pouvons citer entre autres la fiabilité de l’outil de recueil de données, la standardisation de la procédure de de recueil, la variabilité de la population parente...

Influence de la taille d’échantillon sur la marge d’erreur

Comment le nombre de répondants peut influer sur la précision d’une valeur estimée ?

Sans rentrer dans les détails, lors de la conduite d’un test, nous ne pouvons généralement pas interroger l’ensemble de la population parente (question de coût). Sur un échantillon, la valeur n’est mesurée que sur une partie de la population ; on parle donc de valeur estimée. Dans cette estimation, des erreurs peuvent se glisser dont des erreurs liées à l’échantillonnage.

A titre de contre-exemple, sur un recensement, il n’y pas d’erreur d’échantillonnage car (théoriquement) tous les individus de la population sont sollicités. La valeur de la mesure obtenue n’est donc pas une estimation mais la valeur “réelle” (on parle également de “norme”).

Revenons à notre marge d’erreur.

La valeur mesurée lors d’un test est donc soumise aux erreurs d’échantillonnage. Ces erreurs d’échantillonnage entraîne de la variabilité entre les mesures observés sur différents échantillons.

Par exemple, en sélectionnant un petit échantillon de 10 personnes, si par “malchance” un ou deux répondants ont des valeurs “extrêmes” par rapport à la tendance générale, ces répondants “faiblement représentatif” de la population ont pourtant un fort pouvoir biaisant sur la valeur observée (contribution à hauteur de 10% par individu).

Certains d’entre vous penseront et ils n’auront pas tort :

“OK, c’est bien beau tout ça mais c’est très théorique…

Comment je fais, moi, concrètement pour déterminer le nombre de répondants minimum m’assurant une confiance acceptable envers les résultats obtenus ?”

Détermination du nombre minimum de participants

Bien entendu, la marge d’erreur tolérée dépend, en premier lieu,  des objectifs de l’étude et de la pertinence/du besoin d’obtenir une valeur estimée très précise vs approximative.

Nous avons vu que la marge d’erreur est directement influencée par le volume de l’échantillon dû à l’erreur d’échantillonnage. Pour connaître le nombre minimum de répondants, déterminons alors la marge d’erreur maximale acceptable.

Nous avons donc fait figurer l’évolution de la marge d’erreur en fonction du nombre de répondants pour une mesure de type moyenne sur une échelle de notation (issue d’une variable numérique) et pour une mesure de type pourcentage de répondants (issue d’une variable catégorielle).

Cas d’une variable numérique

L’utilisation de variable numérique permet d’obtenir une mesure quantitative du phénomène étudié via le calcul d’une moyenne et d’une variabilité (écart-type).

Dans ce cas la marge d’erreur se calcule en fonction de l'écart-type observé, du nombre de répondants et du niveau confiance choisi au préalable (95%).

Pour étudier l’évolution théorique de la marge d’erreur associée à une moyenne, nous postulons le cas simple d’une mesure sur une échelle d’évaluation de 0 à 100. Imaginons une moyenne observée de 50 et un écart-type de 10.

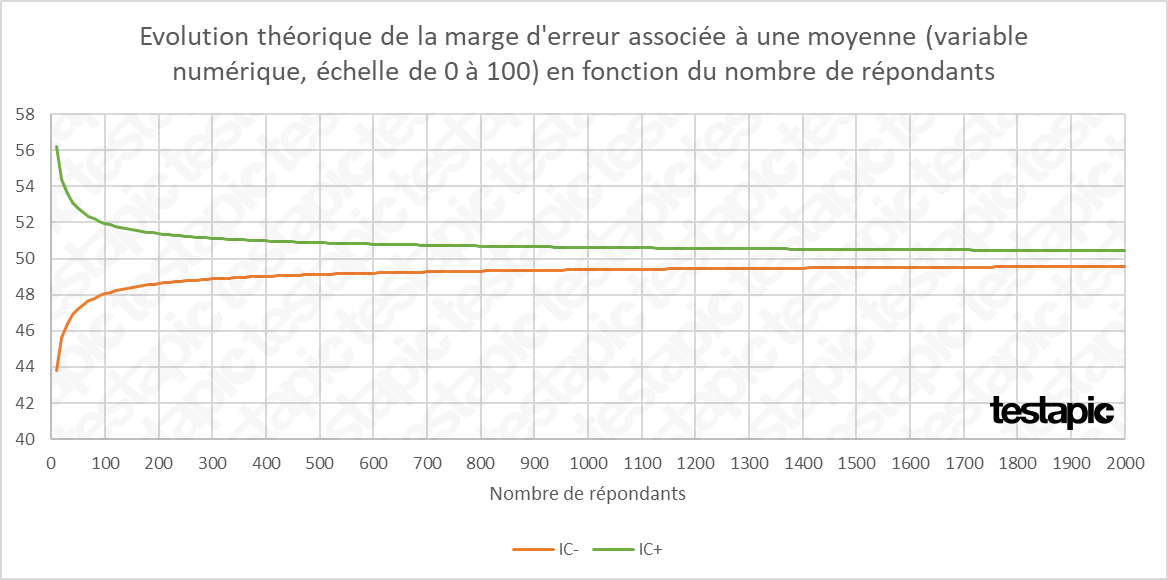
A titre indicatif, sur la variable numérique fictive étudiée ici, la marge d’erreur est de 6,2 (sur une échelle de 100) pour un échantillon de 10 répondants. Elle descend à :

• 2,8 pour 50 répondants,
• 2,0 pour 100 répondants,
• 1,6 pour 150 répondants,
• 1,4 pour 200 répondants et
• 1,1 pour 300 répondants.

Cas d’une variable catégorielle

Lorsqu’on utilise une variable catégorielle, nous recueillons généralement la fréquence d’occurrence du choix des items par les utilisateurs. Cette mesure se traduit simplement par un pourcentage d’utilisateurs ayant choisi l’item “x” parmi un ensemble d’items proposés.

Pour illustrer l’évolution théorique de la marge d’erreur associée à un pourcentage, nous postulons le cas simple d’une valeur observée de 50%.

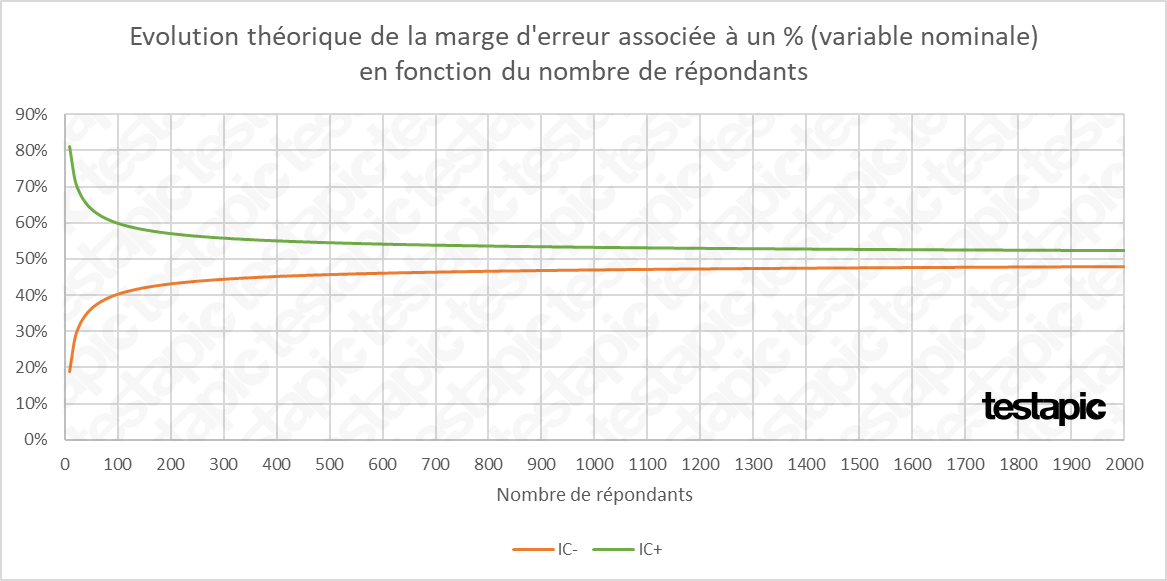
La marge d’erreur associée à notre pourcentage de répondants est de 31% pour un échantillon de 10 répondants. Elle descend à :

• 24% pour 50 répondant,
• 10% pour 100 répondants,
• 8% pour 150 répondants,
• 7% pour 200 répondants et
• 6% pour 300 répondants.

Vous me direz : “OK, c’est un peu plus concret, mais ça reste théorique…”

Je vous répondrai “C’est pas faux… Prenons alors un cas d’étude !”

Exemple issu d’un jeu de données réelles

Prenons pour exemple un cas concret ; nous disposons d’un jeu de données de 250 utilisateurs ayant répondu à la question suivante :

“Quelle note de satisfaction (de 0 à 10) donnez-vous globalement à votre opérateur Internet ?”

Nous traiterons les résultats de cette question sous 2 angles :

• à l’aide d’une variable numérique (note donnée par les utilisateurs de 0 à 10)
• à l’aide d’une variable catégorielle (valence de la note : note positive [de 7 à 10] / note négative [de 0 à 6])

Etape 1 : Résultats pour l’ensemble des 250 répondants

Les résultats obtenus sur l’ensemble de l’échantillon nous servirons de valeurs de “référence” pour la suite de la démonstration.

Sur le jeu de données entier, nous obtenons les résultats de “référence” suivants.

La variable numérique traitée ici correspond à la note en elle-même (de 0 à 100) donnée par les répondants :

• Nombre d’observations = 250
• Moyenne = 7,26
• Ecart-type = 1,96
• Marge d’erreur = 0,24
• Intervalle de Confiance de 95% ; IC(95) = [7,01 ; 7,50]

La variable catégorielle traitée ici correspond à la valence de la note donnée par les utilisateurs (note positive [de 7 à 10] vs note négative [de 0 à 6]).

Nous nous intéressons à la mesure concernant les “notes positives” ; les données concernant l’échantillon global sont les suivantes :

Variable catégorielle nominale (% de notes positives) :

• Nombre d’observations = 250
• % notes positives = 70,4%
• Marge d’erreur = 6,2%
• Intervalle de Confiance de 95% ; IC(95%) = [64,2% ; 76,6%]

Etape 2 : Mise en évidence de la variabilité entre les échantillons

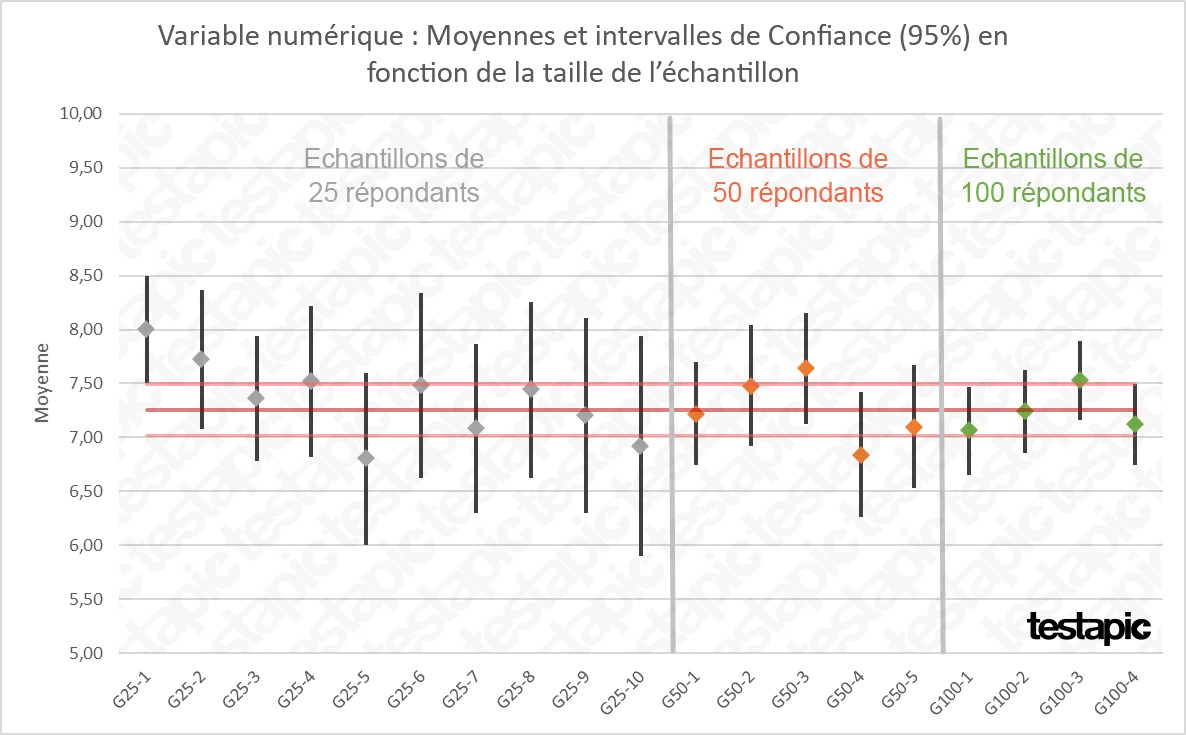
Nous avons ensuite subdivisé, de manière aléatoire, l’échantillon global en plusieurs groupes, tout en faisant varier le nombre d’observations par groupe, de la manière suivante :

• 10 groupes de 25 observations (G25-1 à G25-10 ; en gris dans les graphiques ci-dessous)
• 5 groupes de 50 observations (G50-1 à G50-5 ; en orange)
• 2 groupes de 100 observations (G100-1 et G100-2 ; en vert)
• une seconde subdivision de 2 groupes de 100 observations (G100-3 et G100-4 ; en vert)

Pour chaque groupe issu de la subdivision de l’échantillon global, nous avons recalculé les notes moyennes afin de les comparer entre eux et à notre “référence” calculée précédemment (échantillon entier de 250 observations ; moyenne = 7,26 et IC(95%) = [7,01 ; 7,50], en rouge dans le graphique ci-dessous).

De même pour la variable catégorielle (“notes positives”) qui nous donne comme mesure finale un pourcentage de répondants. Nous procédons exactement de la même manière que précédemment (subdivision aléatoire de l'échantillon global en groupes de 25, 50 et 100 observations).

Pour chaque groupe issu de la subdivision de l’échantillon global, nous avons recalculé les % de notes positives afin de les comparer entre eux et à notre “référence” calculée précédemment (échantillon entier de 250 observations ; % de notes positives = 70,4% et IC(95%) = [64,2% ; 76,6%], en rouge dans le graphique ci-dessous).

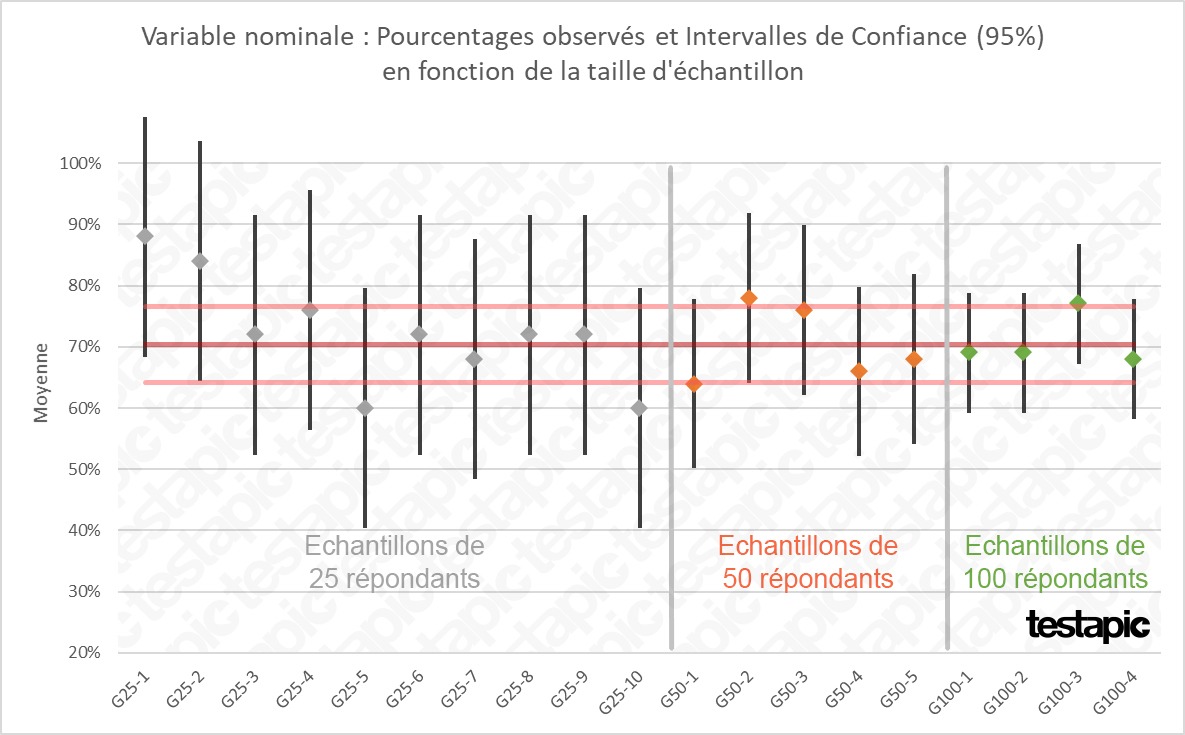
Les 2 graphiques présentés ci-dessus nous montrent l’impact direct du nombre de répondants sur la valeur observée et les marges d’erreur associées.

Avec des échantillons de 25 répondants, dans 2 cas sur 5 la valeur observée ne se situe pas dans l’intervalle de confiance de “référence” (issu de l’échantillon global de 250 répondants).

La valeur observée est également hors de l’intervalle de confiance dans 2 cas sur 5 avec des échantillons de 50 répondants mais les valeurs observées (note moyenne et % de répondants) sont plus proches de l’intervalle de confiance de “référence”.

Avec des échantillons de 100 répondants, la valeur observée est hors de l’intervalle de confiance de “référence” dans 1 cas sur 4 et, dans tous les cas, cette valeur est très proche de l’intervalle de confiance de “référence”.

CONCLUSION

L’exemple que nous venons de traiter est assez parlant. Les comparaisons des résultats obtenus en fonction de la taille des échantillons montre qu’en augmentant le nombre de répondants :

• la valeur observée (moyenne ou le pourcentage de répondants) varie moins par rapport à la mesure de référence,
• la marge d’erreur de l’intervalle de confiance diminue.

Ainsi, plus vous avez d’observations, plus votre valeur observée est précise et proche de la valeur “réelle”.

Les données de l’exemple traité ici montre également que les variations des valeurs observées commencent à être minimes et deviennent acceptables à partir de 100 observations.

Cet enseignement est également à prendre en compte lorsque l’on souhaite segmenter (a priori ou a posteriori) l’échantillon global en fonction de profils utilisateurs par exemple. Corollairement à ce que nous venons de voir, plus vous segmentez votre échantillon, moins les mesures sont précises.

Copyright icone : Magicon